数值平均分布区间划分算法
1. 问题背景
我们首先看京东搜索价格区间的示例:
在京东搜索输入关键词"手机"时,京东聚合出来的价格筛选区间为:

输入关键词"手机 iphone",聚合出来的价格筛选区间为:

输入关键词"手机套 iphone",聚合出来的价格筛选区间为:

可以看到这三次搜索的价格区间完全不同,如果点击这些价格区间,就会发现每个区间的商品数目基本相同。这样做的好处是:区间更加友好,便于用户选择。以关键词手机的价格区间为例,如果有新增一个区间0-50,并且这个区间只有一个商品,那么这样的区间就没有存在的意义,应该合并到后面的区间。
价格区间是根据符合条件的所有商品的价格动态聚合出来的,一旦商品发生变化,对应的价格区间也会发生变化。如何实现这样的需求呢?
2. 最笨、最直接的方法
把所有符合条件的商品的价格都查询出来,放在内存中,排序后,再截取相应的区间段。这样做的缺点有:
- 效率问题。如果符合条件的商品有1w条,通常分页查询只会返回30条数据。现在需要把1w个商品的价格都查询出来加载在内存中,然后使用快速排序算法排序后再划分响应的价格段。对内存、CPU、IO的消耗都是比较大的,基本上每次商品搜索都会做价格区间聚合,如果每分钟有100乃至1000次这样的请求,系统的开销是巨大的。
- 聚合出来的区间不够美观。采用实际的商品价格作为区间,商品的价格可能会小数、单位数等,通常价格区间都是10、20、50、100...的倍数。
3. 平均分布区间划分算法
在介绍算法之前我们需要先了解一些数理统计的概念和方法。
3.1. 数理统计理论基础
- 方差、标准差
标准差(Standard Deviation,SD),在概率统计中最常使用作为测量一组数值的离散程度之用。标准差定义为方差的算术平方根,反映组内个体间的离散程度。假设有一组数值X₁,X₂,X₃,......Xn(皆为实数),其平均值(算术平均值)为μ,则标准公式为:
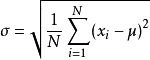
方差(Variance)是标准差的平方。
- 置信区间 *
在统计学中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。置信区间展现的是,这个总体参数的真实值有一定概率落在与该测量结果有关的某对应区间。置信区间给出的是,声称总体参数的真实值在测量值的区间所具有的可信程度,即前面所要求的“一定概率”。这个概率被称为置信水平。对置信区间的计算通常要求对估计过程的假设(因此属于参数统计),比如说假设估计的误差是成正态分布的。
对于一组给定的样本数据,其平均值为μ,标准偏差为σ,则其整体数据的平均值(1-α) 置信区间为 (μ-Ζα/2σ , μ+Ζα/2σ),其中α为非置信水平在正态分布内的覆盖面积 ,Ζα/2 即为对应的标准分数,可以查表得到:
| 置信水平1-α | 对应标准分数Zα/2 |
|---|---|
| 95% | 1.96 |
| 90% | 1.65 |
| 80% | 1.28 |
3.2. 结论
假设一组1000个商品的平均价格为100,标准差为20,根据上面的理论有如下的统计学结论:
- 该组中任何一个商品的价格有95%的概率在区间:(100-20*1.96, 100+20*1.96)=> (60.8,139.2);90%的概率在区间:(100-20*1.65, 100+20*1.65)=> (67,133.2)。
- 对该组商品价格来说,区间(60.8,139.2)应该包含了95%的商品(约950个商品),区间(67,133.2)应该包含了90%的商品(约900个商品)。
对于搜索平台来说,取置信水平95%。
3.3. 算法步骤
- 统计符合条件的商品集合的平均值、标准差,并计算95%概率的置信区间
上面例子中的区间为(60.8,139.2) - 对上面的商品集合来说,95%的商品的价格位于(67,133.2)区间。设定一个均分系数m,将区间划分成m*size个子区间,然后统计各个子区间的商品数。
如果取均分系数为5,size为6,则将区间(67,133.2)等分成30个子区间,还有两个端点区间(0, 67)、(133.2, ⑅)并统计这32个子区间的商品数。 - 根据计算到的m*size+2个子区间的商品数目,在尽量保证商品数目相等的原则下,将子区间合并为size个区间。
- 对计算到的size个区间进行平滑处理,避免[20, 32.5)这样的区间范围。
3.4. 算法结果展示
通过本算法实现的价格筛选区间示例:

